Cours et TD Electronique-Electrotechnique et Automatique
Cours : L’Amplificateur opérationnel (AOP – ALI)
4 ans ago 5 min read
Nombre de vues :9 017
1-Présentation de l’AOP :
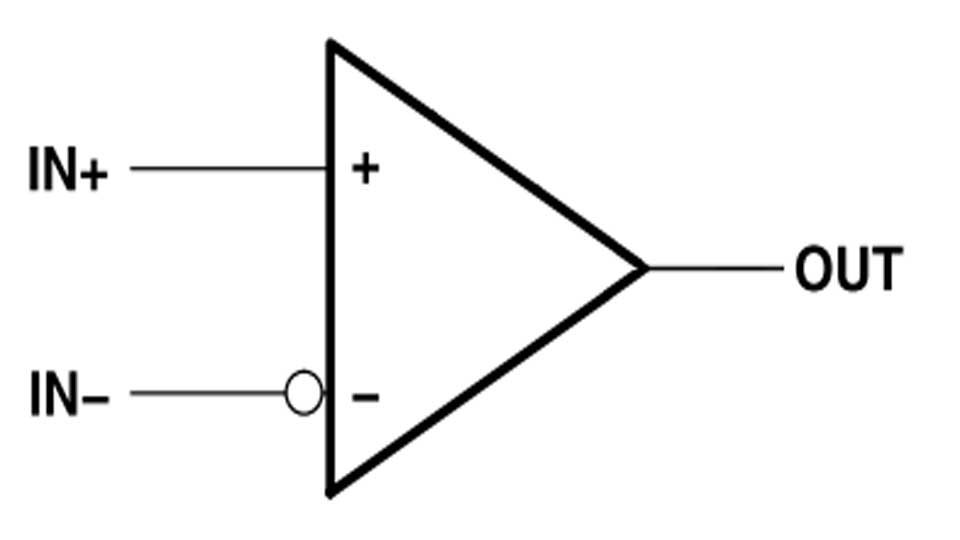
L’amplificateur opérationnel( ou amplificateur linéaire intégré: ALI )est un composant en technologie intégrée qui est prêt à être opérationnel, ce composant comporte:
– 2 broches d’alimentations +Vcc et -Vcc,
-2 entrées dites différentielles: E + entrée non inverseuse et E–entrée inverseuse,
-Une sortie S .
Le fonctionnement de l’amplificateur opérationnel impose une alimentation symétrique ( deux sources de tension + Vcc et – Vcc, qu’on ne représente pas sur les schémas).
On appelle tension différentielle (qu’on note ε), la ddp entre l’entrée v+et v–
ε= v+ – v–
Symbole de l’Aop
La tension de sortie a pour expréssion : Vs = A. ε ( A: représente l’amplification différentielle) .
L’Aop a deux modes de fonctionnement :
Mode ( ou régime)linéaire : on a forcément une contre-réaction négative ( liaison par composant ou un simple fil entre la sortie S et l’entrée E–de l’Aop) , dans ce cas la tension ε sera négligée .
Mode( ou régime)non linéaire : il y a pas de contre réaction négative, dans ce cas l’Aop fonctionne en saturation.
Dans ce cas la tension sortie ne peut prendre que deux valeurs : +Vsatou –Vsat, la tension ε ne peut être négligée.
2) Amplificateur opérationnel parfait ( ou idéal)
Ce modèle permet de prévoir le comportement de l’amplificateur :
Le modèle de l’AOP idéal comporte:
– Une résistance d’entrée différentielle infinie, ce qui implique ==> i+ = i– = 0.
-Une amplification différentielle( en boucle ouverte) A infinie , quelque soit la fréquence.
Quand la tension différentielle est nulle la tension de sortie ne l’est pas, ce qui fait que l’AOP présente une tension de décalage en sortie
en absence de tout signal à l’entrée.
Caractéristique de transfert réelle
b) Le slew rate (SR)
La pente en valeur absolue de dVs/dt , qui informe sur la vitesse d’évolution de la tension du signal de sortie Vs de l’AOP, est limitée par une valeur maximale: ce slew rate caractérise la rapidité de réponse de l’AOP et s’exprime en V /µs ( pour l’AOP TL081 SR = 13 V/µs).
Donc pour augmenter la rapidité de réponse de l’AOP , il faut réduire l’amplitude des tensions d’entrées.
4) L’Amplifiacteur opérationnel en régime linéaire
En régime linéaire ( il y a présence d’une contre-réaction négative) on supposera que
: i+ = i– = 0. et ε = 0 c’est à dire v+ = v–
a) Montage suiveur
La tension différentielle ε = 0 en appliquant la loi des mailles, on peut écrire : VE – ε- VS = 0 ==> VS =VE – ε
VS =VE
L’intérêt de ce montage réside dans sa résistance d’entrée infinie et sa résistance de sortie nulle, on l’utilise souvent pour adapter deux étages.
b) Montage non-inverseur
On a bien une contre réaction négative ==> ε = 0 ==> VE= v+ = v–= VR1 en appliquant le principe de diviseur de tension on a :
VE= VS.R1/(R0+ R1) ce qui donne :
c) Montage inverseur
On a bien une contre réaction négative ==> ε = 0 En appliquant le théorème de Millman on a :
v–= [VE/ R1 + VS/ R0]/ ( 1/ R1+1/R0 ) ce qui donne :
Autre démonstration, On a : VE=R1.I, car le potentiel v–=0 V (car v+ = 0 V, et ε = 0 donc v+ = v–= 0 V)
de même Vs= – R0.I ( i– = 0)==> VS/VE=- (R0/R1).
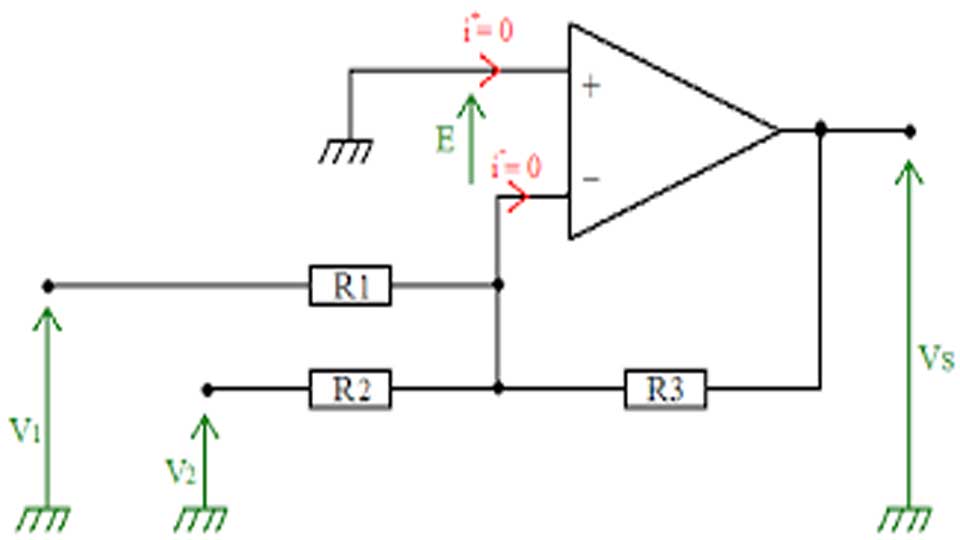
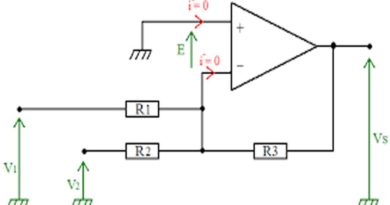
d) Amplificateur soustracteur
On a bien une contre réaction négative ==> ε = 0==> v+ = v– avec v+= v–et VR3 = v+= v–.
en appliquant le principe de diviseur de tension on a :VR3= V2.R3/(R2+ R3) et en appliquant le théorème de Millman on a :
On a bien une contre réaction négative ==> ε = 0 et v+ = 0V ==> v– = 0V
en appliquant le théorème de Millman on a : v–= [V1/R1+V2/R2+V3/R3+ Vs/R0] / [1/R0+1/R1+1/R2+ 1/R3]= 0 ce qui donne :
Et si on prend R0 = R1=R2=R3 on a :
VS = – (V1+V2+ V3)
On peut éliminer le signe – en ajoutant un étage inverseur ( avec deux résistances identiques) à la sortie de l’amplificateur sommateur.
5) Autres circuits de bases
On a deux autres circuits de base : les circuits intégrateur et dérivateur, ces circuits agissent sur le spectre des signaux .
Car leur réponse ne sera pas la même selon la fréquence des signaux.
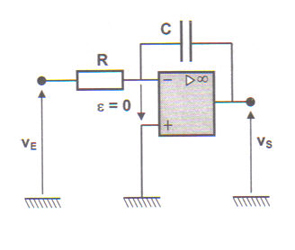
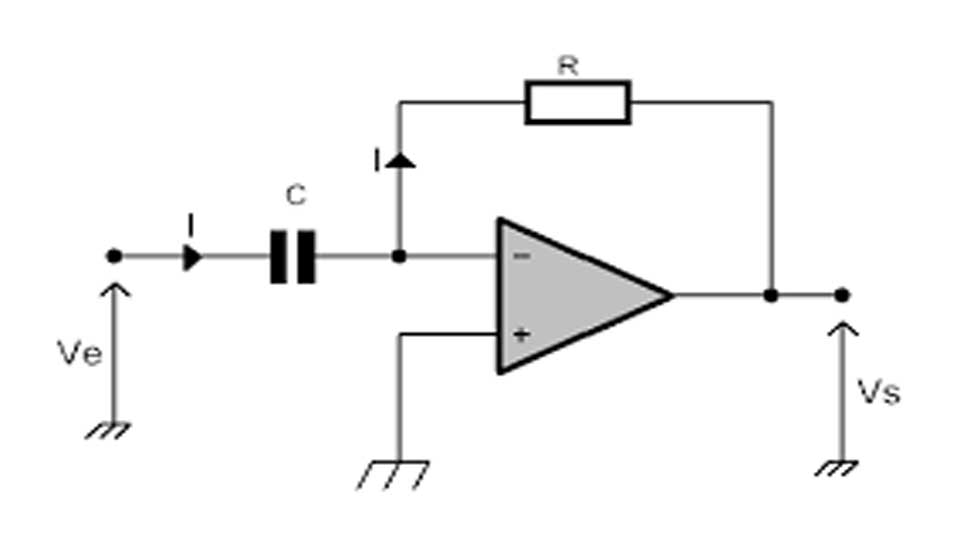
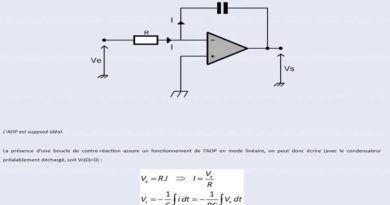
a) Montage intégrateur
On a bien une contre réaction négative ==> ε = 0 et v+ = 0V ==> v– = 0V et i+ = i– = 0.
Ce qui fait que la résistance et le condensateur C sont parcourus par le même courant i.
En régime variable : on a VE(t)=R.i(t) et i(t) = – C dVs / dt ==>VE(t)= -R.C dVs / dt ==> : dVs / dt =-1/(R.C). VE(t)
On constate que le condensateur est alimenté par le courant i= , indépendant de C , le circuit réalise une intégration parfaite.
Vs(t) = -1/(R.C).∫VE(t).dt
Vs(t) = -1/(R.C).∫VE(t).dt + Vs(0)
En régime sinusoïdal: On utilise la notation complexe, on aVS = –VE(Zc/R) = -VE. 1/ ( jRCω) ( Zc= 1/ jCω) finalement on a :
VS = –VE. 1/ ( jRCω)
Exemple 1: Soit une tension carrée d’amplitude 2V et de fréquence 1 kHz, avec R = 10 kΩ et C = 10 nF, on prend Vs(0)= -5V.
F = 1 kHz == la période du signal est T = 1/F = 1/1000 = 1 mS. ==> R.C=10-4s
Pour 0<t< 0.5mson a VE(t)= – 2V ==>Vs(t) = -1/(R.C).∫VE(t).dt + Vs(0).
les bornes d’intégrations sont 0 et t ce qui donne : Vs(t) = -1/(10-4).∫-2.dt + (-5) = 20000t – 5 ==>
Vs(t)=20000t – 5
Pour 0.5 ms<t< 1 mson a : VE(t)= + 2V , Vs(t) = -1/(10-4).∫2.dt = – 20000t + K
A t = 0,5 ms Vs(t) = 5 V ==> Vs(0,0005) =- 20000×0,0005+K = -10+K = Vs(0,0005) lorsque 0<t< 0.5ms
ceci par continuité de Vs(t) au point t = 0,0005 S.
Pour 0<t< 0.5ms on a Vs(0,0005)= 20000×0,0005-5 = 10- 5 = 5V = -10 + K ==> K = 15 V.
Finalement on a :
Vs(t)=-20000t+15
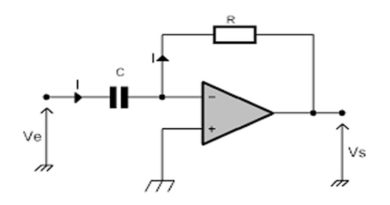
b) Montage dérivateur
On peut mener la même étude avec :
Vs=-R.i et i = C.dVe/dt car la tension Ve se retrouve aux bornes du condensateur C ( AOP en régime linéaire, suite à la présence d’une contre-réaction négative : R).
Donc finalement Vs= – R.i= -R.CdVe/dt ( on a bien un signal de sortie Vs proportionnel à la dérivée du signal d’entrée Ve).
Plus d'articles
TD1 : Amplificateur opérationnel linéraire ( AOP)
Exercice : étude d’un circuit dérivateur
Exercice : Circuit intégrateur à base d’AOP