Exercice corrigé filtre Passe-bas de Butterworth
On rappelle que seule l’étude théorique du filtre passe-bas est faite. On passe aux autres types, passe-haut, etc.. par changement de variable.
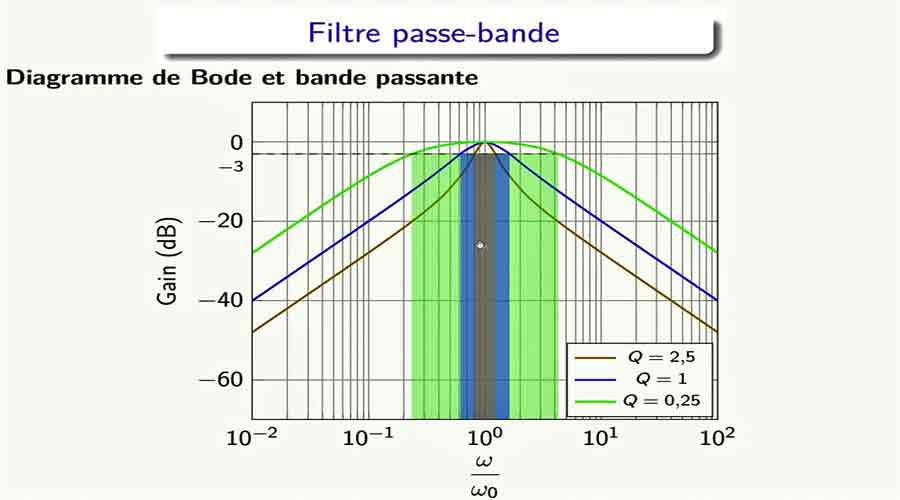
Le filtre de Butterworth d’ordre n est défini par le module au carré de sa fonction de transfert selon : H = H0 /(1+(f/f0)2n)1/2.
On montre aisément que quel que soit l’ordre n du filtre, le gain à la fréquence est toujours de -3 dB. On admettra que c’est le filtre de Butterworth qui permet sur l’ensemble des types standardisés de filtres d’obtenir la réponse la plus plate dans la bande passante.
La problématique théorique du filtre de Butterworth consiste à établir pour un ordre n donné en fonction du gabarit du filre souhaitée.
Le filtre de Butterworth d’ordre n est défini par le module au carré de sa fonction de transfert selon : On montre aisément que quel que soit l’ordre n du filtre, le gain à la fréquence est toujours de -3 dB.
Un filtre est linéaire si les tensions d’entrée et de sortie sont reliés par une équation différentielle linéaire. ϕ = ϕs − ϕe est la déphasage de vs par rapport à ve.
Exercice : Filtre analogique de Butterworth
Correction exercice : Filtre analogique de Butterworth
Sujets similaires:
Exercice avec correction : Etude d’un filtre Passe bande – Calcul de la bande passante
Exercice : Filtre de Sallen & Key de type passe-bande
Exercice : Fonction de transfert d’un filtre passe-haut de Sallen & Key
Exercice corrigé : Détermination de la fonction de transfert à partir de la représentation d’état
Réponse temporelle d’un filtre linéaire à un signal périodique
