Exercice Corrigé sur le filtre numérique – Réponse impulsionnelle – Réponse indicielle

un filtre numérique est un dispositif électronique qui effectue un filtrage à l’aide d’une succession d’opérations mathématiques sur un signal discret. C’est-à-dire qu’il modifie le contenu spectral du signal d’entrée en atténuant ou éliminant certaines composantes spectrales indésirées.

Contrairement aux filtres analogiques, qui sont réalisés à l’aide d’un agencement de composantes physiques (résistance, condensateur, inductance, transistor, etc.), les filtres numériques sont réalisés soit par des circuits intégrés dédiés, des processeurs programmables (FPGA, microprocesseur, DSP, microcontrôleur, etc.), soit par logiciel dans un ordinateur.

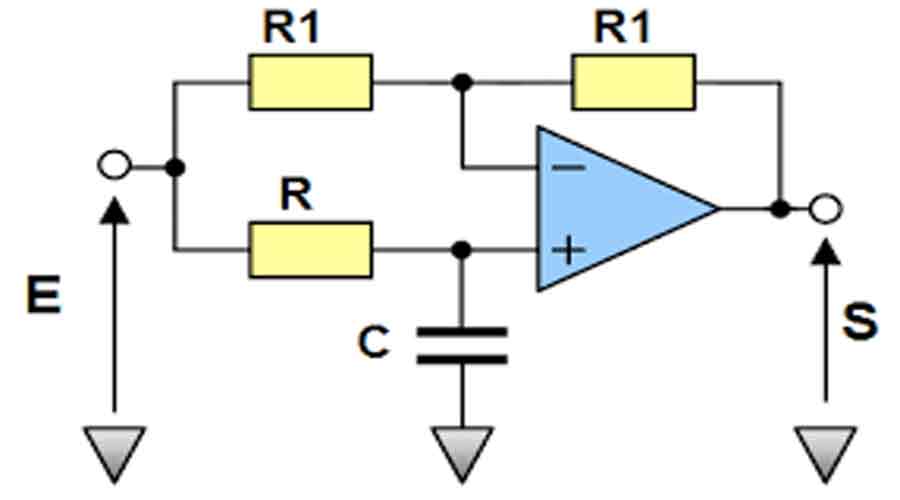
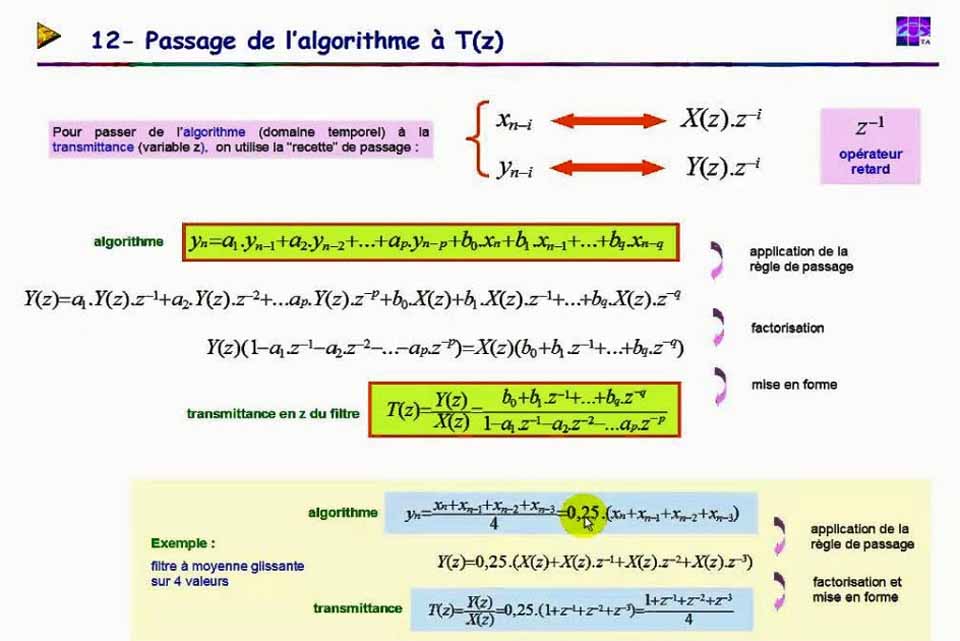
Un filtre numérique peut être défini par une équation différentielle, c’est-à-dire l’opération mathématique du filtre dans le domaine temporel (discret). Exemple :

Si l’on dispose de Matlab c’est bien sûr encore plus simple. On utilise la fonction c2d avec l’argument ‘zoh’ pour “zero holder hold” (bloqueur d’ordre zéro).
Matlab
% Définition d’un système continu :
sysc=tf(1,[1 1]);
% Obtention de la transformée en z du système échantillonné à Te
Te=0.1;
sysd=c2d(sysc,Te,’zoh’);
% Notation en z^-1
sysd.variable=’z

. Le script Matlab ci-dessous montre la création des
deux systèmes :
Matlab
% Définition de deux systèmes continus :
sys1=zpk([],[-1-2i -1+2i],2^2+1);
sys2=zpk([],[-1-(2+2*pi)*i -1+(2+2*pi)*i],1+(2+2*pi)^2);

La fonction c2d de Matlab permet d’obtenir l’équivalent discret d’une fonction de transfert continue avec la méthode d’intégration comme argument :
Matlab
sysc=tf([1 0],[1 2 5]);
Te=0.1;
% Méthode d’euler :
sysd1=c2d(sysc,Te,’zoh’);
% Méthode des trapèzes :
sysd2=c2d(sysc,Te,’foh’);
% Méthode bilinéaire :
sysd3=c2d(sysc,Te,’tustin’);

On utilise la fonction c2d avec l’argument ‘zoh’ pour “zero holder hold” (bloqueur d’ordre zéro).
Matlab
% Définition d’un système continu :
sysc=tf(1,[1 1]);
% Obtention de la transformée en z du système échantillonné à Te
Te=0.1;
sysd=c2d(sysc,Te,’zoh’);
% Notation en z^-1
sysd.variable=’z

La fonction c2d de Matlab permet d’obtenir l’équivalent discret d’une fonction de transfert continue avec la méthode d’intégration comme argument :
Matlab
sysc=tf([1 0],[1 2 5]);
Te=0.1;
% Méthode d’euler :
sysd1=c2d(sysc,Te,’zoh’);
% Méthode des trapèzes :
sysd2=c2d(sysc,Te,’foh’);
% Méthode bilinéaire :
sysd3=c2d(sysc,Te,’tustin’);

Exercice : Filtre numérique : 

Exercice : Filtre numérique – Correction :