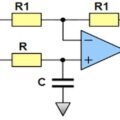
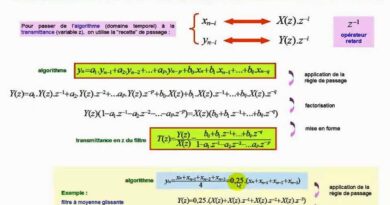
Exercice Corrigé sur la Transformée en Z inverse

5 mai 2025 WikiGelec78

Nombre de vues : 10

Un signal discret s(k) est une séquence de nombres réels appelés échantillons. L’indice k est généralement associé à un instant d’échantillonnage : t = k.Te. La période d’échantillonnage Te est supposée constante.

La fonction de la variable complexe s(z) est une série et ne converge pas forcément pour toute valeur de z. En toute rigueur il faudrait associer le rayon de convergence à chaque fonction en z : {s(z) converge pour |z| > α}.

Le script Matlab permettant de créer un objet Matlab correspondant à une fonction
de transfert discrète est donné ci-dessous.
Matlab
% Création d’un système linéaire discret :
Te=0.1;
sysd = tf([b0 b1 b2],[1 a0 a2 a3],Te,’variable’,’z^-1′);

la fonction de transfert du système peut aussi s’appeler
“réponse impulsionnelle”.
Matlab
% Réponse impulsionnelle d’un système :
[y,t] =impulse(sysd);

le script pour obtenir les
20 premiers échantillons de la réponse indicielle d’un système :
Matlab
% Réponse indicielle d’un système :
[y,t] =step(sysd,20);

Une fonction de transfert est donc aussi bien définie par la donnée de ses pôles et de ses zéros. Le script Matlab pour créer un système ainsi est donné ci-dessous :
Matlab
% Système discret défini par ses pôles et zéros :
Te=0.1;
sysd=zpk([c1 c2 c3],[e1 e2],e0,Te);