Exercice corrigé : Détermination de la matrice de Transition et calculer de l’état d’un système 

Calcul de Φ(t)=e(At) : Il existe plusieurs méthode pour calculer l’exponentielle d’une matrice : utiliser la forme diagonalisable ou à défaut, de Jordan, décomposition de la matrice en élément simple.

Par définition, le système est stable si et seulement si la matrice d’évolution libre A vérifie 0 e (At) → quant t → ∞ .
Théorème : le système est stable si et seulement si toutes les valeurs propres de A (les racines de det(pI-A)) sont à parties réelles strictement négatives.

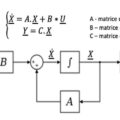
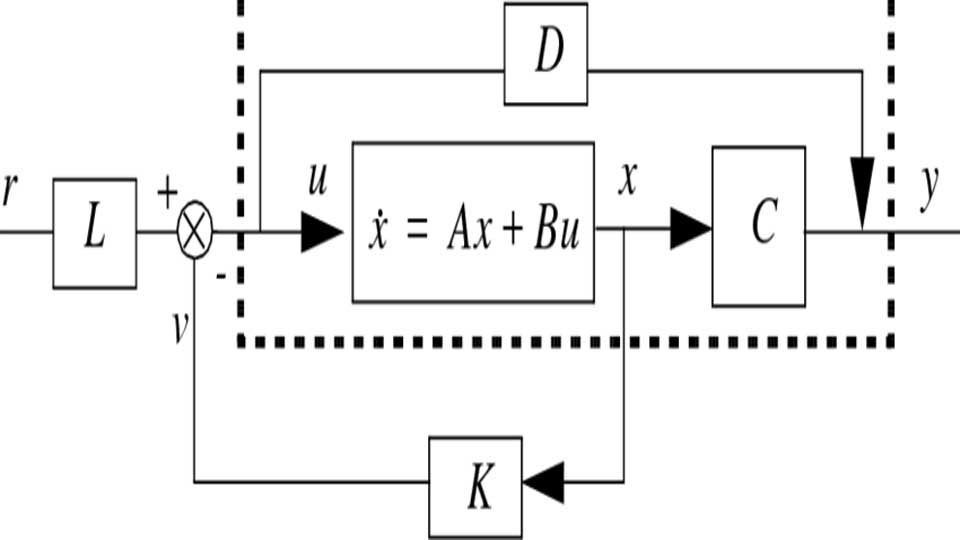
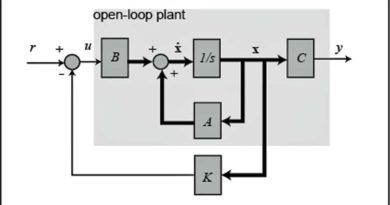
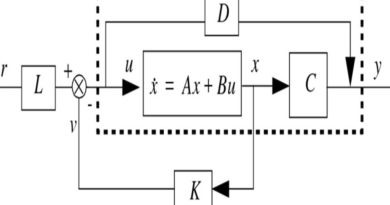
On montre que l’équation différentielle : X ‘(t) = AX (t) + BU(t)  admet une solution entre les instants t0 et t qui se décompose en une somme de deux fonctions : la réponse libre Xl  ne dépendant que des conditions initiales X0 à l’instant t0 et une  réponse forcée Xf ne dépendant que l’entrée U(t) du système : X (t) = Xl (t) + Xf (t) . 

 Exercice : Détermination de la matrice de Transition et calculer de l’état d’un système 

Correction Exercice : Détermination de la matrice de Transition et calculer de l’état d’un système 

Sujets similaires:

Exercice corrigé : Détermination de la fonction de transfert à partir de la représentation d’état TP : Commande par retour d’état d’un système, sous PSIM Exercices : Calcul des erreurs de position et de vitesse d’un système asservi Exercices corrigés sur la commande par retour d’état TD : Représentation d’état d’un système asservi avec Correction