Exercice Corrigé sur le placement de Pôles et l’Observateur d’etat d’un système asservi

Le placement de pôles permet de modifier la dynamique d’un système linéaire. La méthode d’Ackermann calcule le gain de retour d’état à partir des pôles désirés. Elle est utilisable si le système est entièrement commandable.

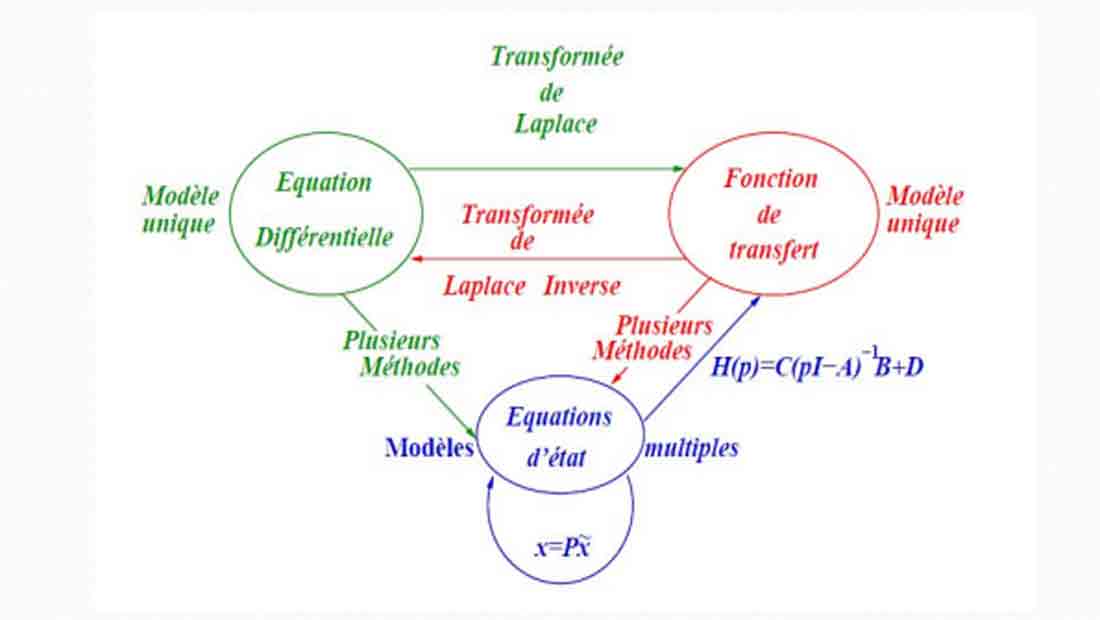
Forme générale du système

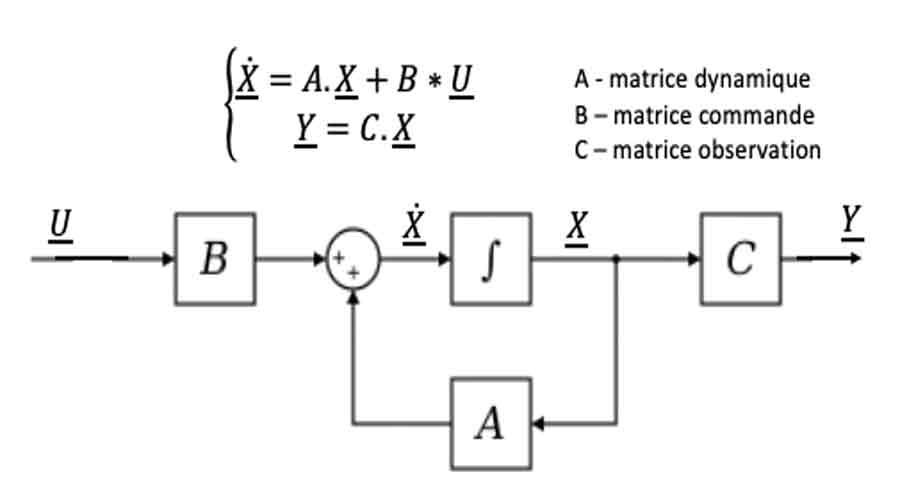
On considère un système linéaire de la forme :

x' = A x + B u

où A est la matrice d’état, B est la matrice de commande, x l’état, u la commande.

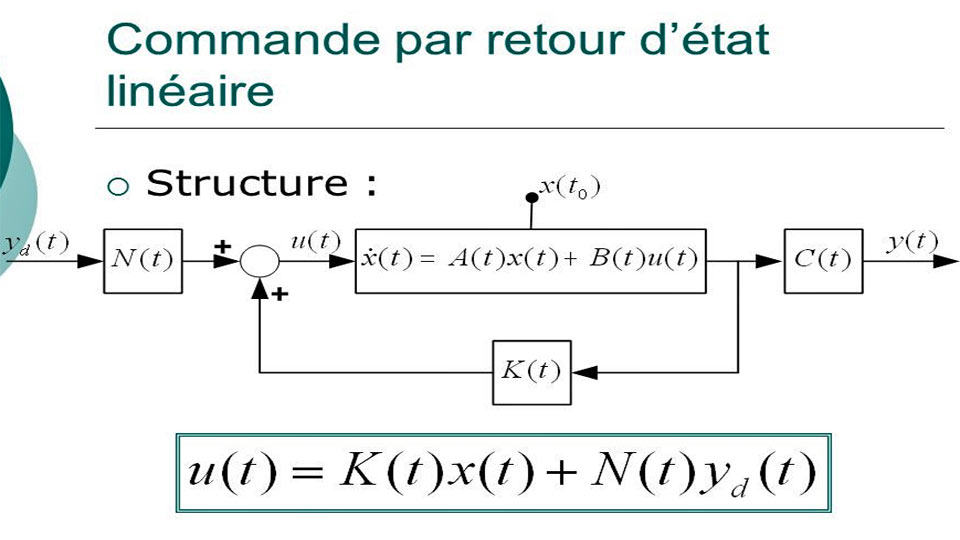
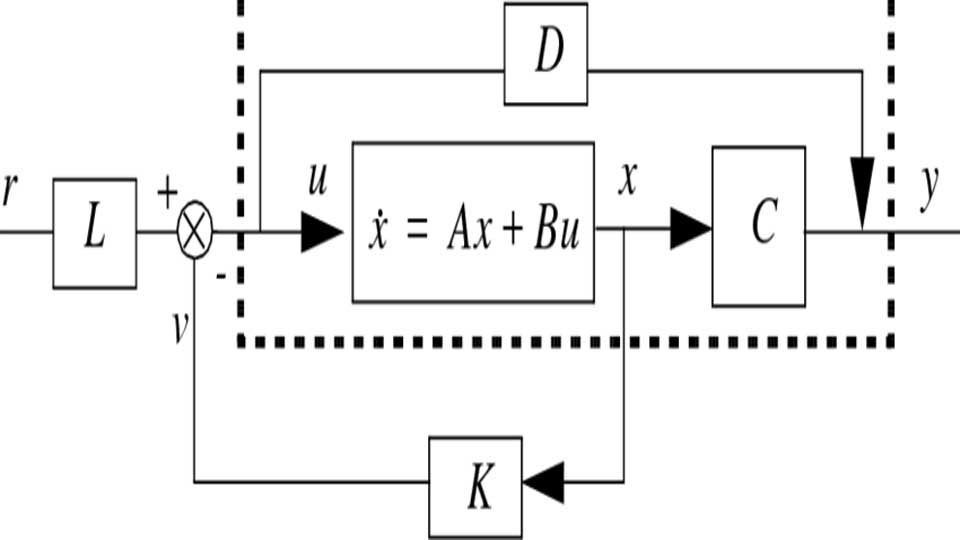
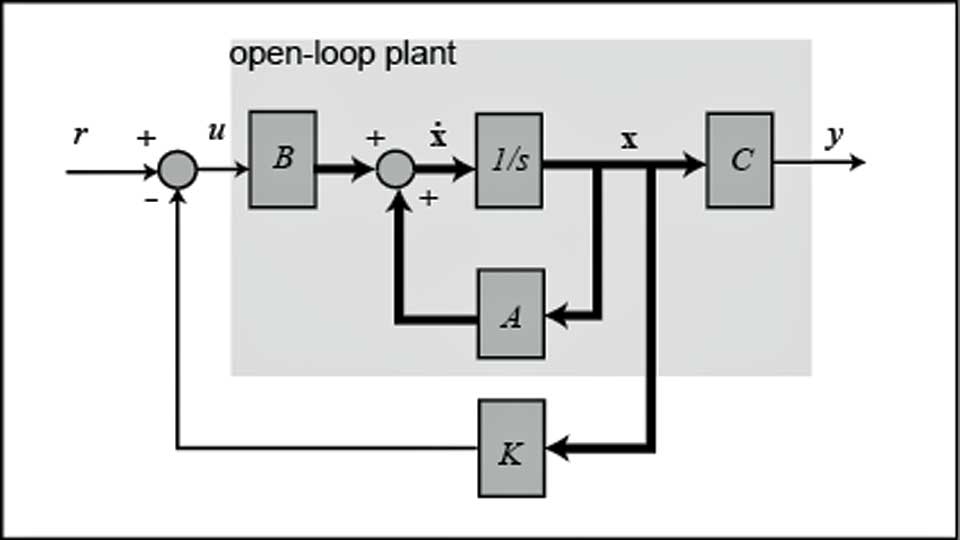
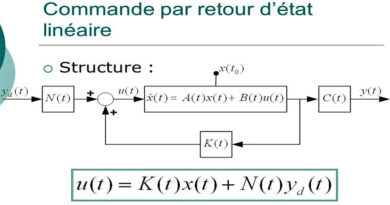
La commande d’état prend la forme u = -K x, ce qui donne le système fermé :

x' = (A - B K) x

---

Condition de commandabilité

Avant d’utiliser Ackermann, vérifiez la commandabilité avec la matrice :

C = [ B | A B | A² B | ... | A puissance (n-1) B ]

Le système est commandable si cette matrice est de rang n.

---

Choix des pôles désirés

Déterminez les pôles désirés du système fermé.

Déduisez le polynôme caractéristique souhaité sous la forme :

s^n + a(n-1) s^(n-1) + ... + a1 s + a0

---

Calcul du polynôme matriciel Phi(A)

On construit :

Phi(A) = A^n + a(n-1) A^(n-1) + ... + a1 A + a0 I

---

Formule de Ackermann

Le gain K est obtenu par :

K = [0 ... 0 1] × C⁻¹ × Phi(A)

Exercice sur le placement de pôles et l’observateur d’etat : 

La Correction :