Exercice1 : Transformée en z inverse

1 mai 2020 WikiGelec78

Nombre de vues : 11 504

La transformation en Z est un outil mathématique de l’automatique et du traitement du signal, qui est l’équivalent discret de la transformation de Laplace. Elle est utilisée entre autres pour le calcul de filtres numériques à réponse impulsionnelle infinie et en automatique pour modéliser des systèmes dynamiques de manière discrète.

Définition : la transformation en Z est une application qui transforme une suite s (définie sur les entiers) en une fonction S d’une variable complexe nommée z, telle que

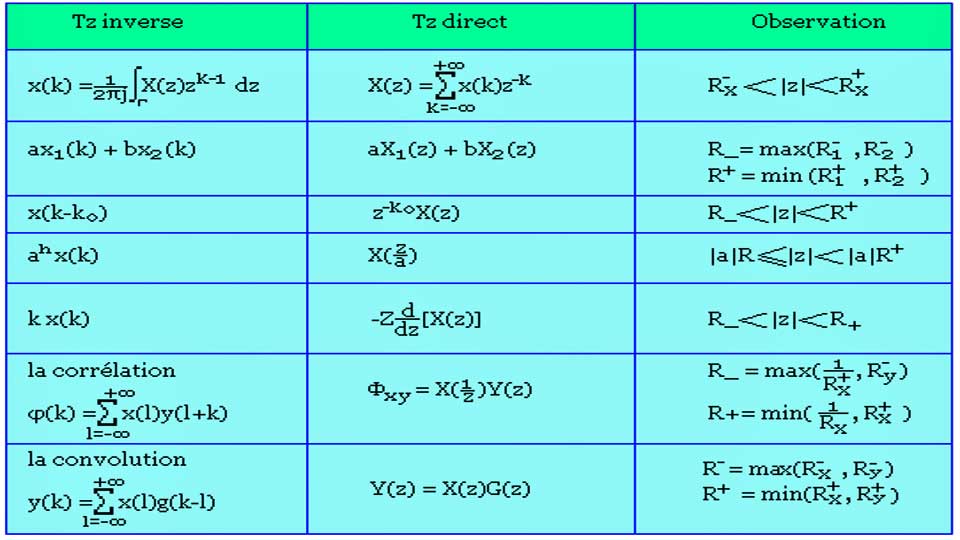
S(z) = \mathcal{Z}\{s(n)\} =\sum_{n=-\infty}^{+\infty}s(n)z^{-n},\quad z \in \left\lbrace z\in\mathbb{C} \Big|\sum_{n=-\infty}^{+\infty}s(n)z^{-n} \quad \mathrm{converge}\right\rbrace

Propriétés de la transformation en Z:

La transformée en Z d’une combinaison linéaire de deux signaux est la combinaison linéaire des transformées en Z de chaque signal.

${\mathcal {Z}}\{a_{1}x_{1}(n)+a_{2}x_{2}(n)\}=a_{1}{\mathcal {Z}}\{x_{1}(n)\}+a_{2}{\mathcal {Z}}\{x_{2}(n)\}\$

Décalage temporel:

Le décalage temporel de k échantillons d’un signal se traduit par la multiplication de la transformée en Z du signal par z^−k.

${\mathcal {Z}}\{x(n-k)\}=z^{{-k}}{\mathcal {Z}}\{x(n)\}.~$

Avance:

Lorsqu’on utilise la transformée en Z monolatérale (voir ci-dessus), on obtient

$\mathcal{Z}_{+}\left\{ x\left( n+k\right) \right\} =z^{k}\left[ \mathcal{Z}_{+}\left\{ x\left( n\right) \right\} -\sum_{j=0}^{k-1}x\left( j\right) z^{-j}\right]$

Convolution:

La transformée en Z d’un produit de convolution est le produit des transformées en Z

$\left( x* y\right) \left( n\right) =\sum_{k=-\infty }^{+\infty }x\left( n-k\right) y\left( k\right)$

Multiplication par une exponentielle:

${\mathcal {Z}}\{a^{{n}}x(n)\}=X\left({\frac {z}{a}}\right)$

avec $X(z)$ transformée en Z de la suite $x(n)$

Multiplication par la variable d’évolution:

De façon générale :

${\mathcal {Z}}\{n^{{k}}x(n)\}=\left(-z{\frac {{\mathrm {d}}}{{\mathrm {d}}z}}\right)^{{k}}{\mathcal {Z}}\{x(n)\}\$

$\textstyle \left(-z{\frac {{\mathrm {d}}}{{\mathrm {d}}z}}\right)^{{k}}{\mathcal {Z}}\{x(n)\}$

signifie que l’on applique k fois à ${\mathcal {Z}}\{x(n)\}$ l’opérateur $\textstyle -z{\frac {{\mathrm {d}}}{{\mathrm {d}}z}}$

Si l’on écrit cette formule au rang k=1, on obtient la formule de dérivation :

${\mathcal {Z}}\{nx(n)\}=-z{\frac {{\mathrm {d}}}{{\mathrm {d}}z}}X(z)\$

Théorème de la valeur initiale:

Soit $x(n)\,$ un signal causal et $X(z)\,$ sa transformée en Z. Alors :

$x(0)=\lim _{{n\to 0}}x(n)=\lim _{{z\to +\infty }}X(z)$

Théorème de la valeur finale:

Soit $x(n)\,$ un signal causal et $X(z)\,$ sa transformée en Z. Alors lorsque la limite de gauche existe, on peut écrire :

$\lim_{n \to +\infty}x(n)=\lim_{z\rightarrow 1,\left\vert z\right\vert >1}(z-1)X(z)$

Exercice :

Correction :